Bricks

A 2D brick procedural shader for a brick wall. This shader is based on this tutorial.

Variable Declarations

    vec3 BRICK_COLOR = vec3(0.5451, 0.1804, 0.0353);
    vec3 MORTAR_COLOR = vec3(0.8784, 0.8667, 0.7373);
    vec2 BRICK_TILE_SIZE = vec2(.08, .03);
    vec2 BRICK_PCT = vec2(.9);
    vec3 color = vec3(0.);

First things first, we declare the different variables we’ll need in order to build the brick wall. Some of these are pretty straight forward, BRICK_COLOR and MORTAR_COLOR which are vec3 describing the colors. The color variable is a vec3 that our function will return after we modify it. Then the two variables that need a few explanations. First BRICK_TILE_SIZE. It describes the size of of a tile, containing a brick and the mortar on the top and right side around it as shown below. The BRICK_PCT variable stands for the brick pourcentage, meaning how much of a brick tile is made up of brick rather than mortar.

Tiling

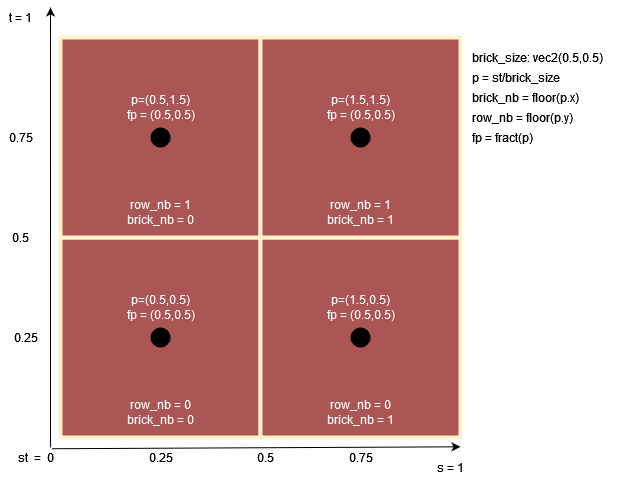
Next step consists of tiling our canvas in order to display more than one brick. For that we’ll use the same logic as explained in the tiling explanation, meaning we will devide our noramlised canvas by the size of a brick tile.

    vec2 position = st/BRICK_TILE_SIZE;
    vec2 norm_position = fract(position)

This gives us as the integral part of the result, the row number for position.y and the brick number for position.x. The fractional part of the result is the normalised position within each brick tile.

Brick Layout Offset

In order to make it look a bit more realistic, the bricks shouldn’t be layed out directly on top of one another, but instead be layed out with an offset on the x axis.

The goal next is to offset position.x every time the row number is odd. To do this we use the code below.

    position.x += step(fract(position.y * 0.5),0.5)/2.;

We are working on non normalised position values, so we need to insert this offset code before we normalise the brick coordinates.

First, let’s break down this part

    fract(position.y*0.5)

The fract() function return the fractional part of a float. On the left fract(y), on the right fract(y*0.5):

The difference is that when y is halved, the fractional part of why covers two rows instead of one. We have a new row of bricks every 0.5, instead of every 1 units. With this new value we can deduce if a row is odd or even, because for even row fract(y*0.5) < 0.5, and for odd rows fract(y*0.5) > 0.5.

All we have to do is use the step() function which returns the 0 or 1 by comparing a given value to a threshold like so:

    step(x,0.5)

In this case if x i 0.2, we get 0, if x is 0.8 we get 1.

So if use the step() function with our new value and compare it to 0.5, we should get a value of 1 every 2 rows. Diagrams are sometimes better than words, and they’re always better than my words, so here:

The blue dotted line represents step(fract(y*0.5),0.5). We can then divide the result of our step(), to create a probable offset.

Color <3

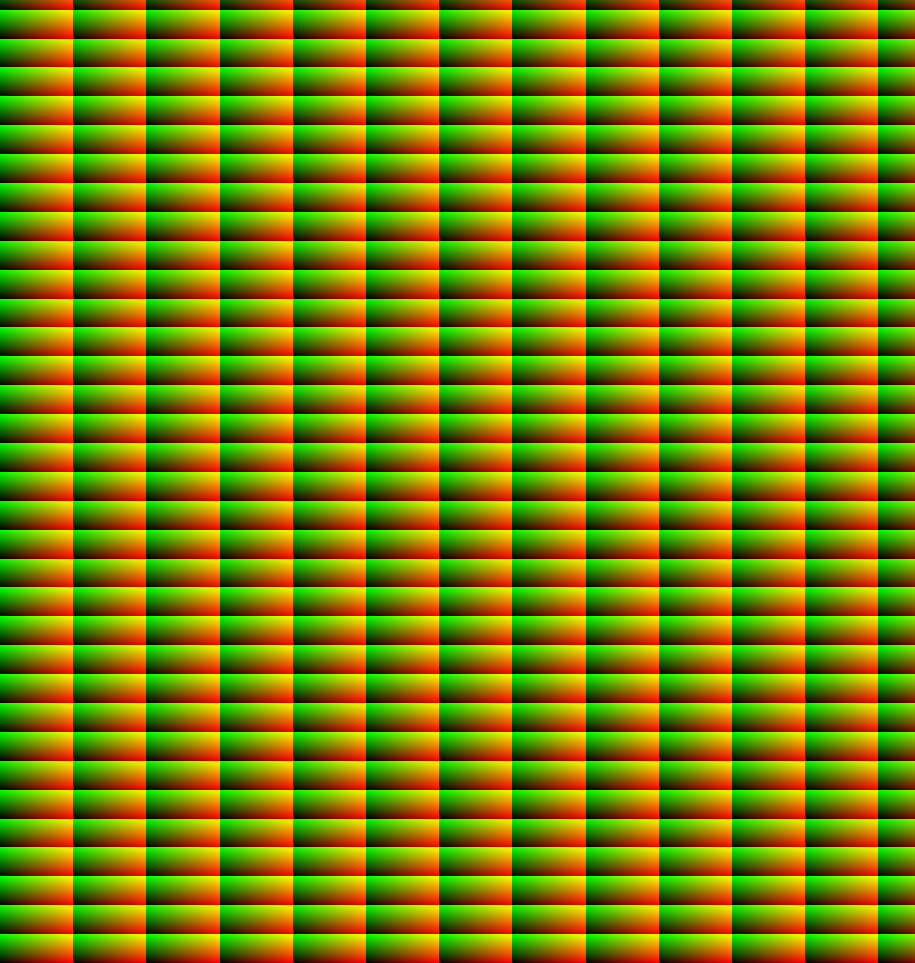
Right now it doesn’t look like much, but we have managed to get normalised coordinates for each brick tile, which means we can at least visualise our coordinates using our color variable.

Rows are going through the green channel: color = vec3(0.,norm_position.y,0.);

Bricks are going through the red channel: color = vec3(norm_position.x,0.,0.);

And together, they look divine:

However this is just a visualisation help, not anywhere near the real colors we need.

The tricky part here is that we don’t want our entire brick tile to be brick colored. We also want to apply the mortar color to the right coordinates.

And that’s where our BRICK_PCT comes in handy. Because it’s a pourcentage, a value between 0 and 1, just like our normalisse coordinates, we can use step() again. This time we will use BRICK_PCT as the threshold against wich we check norm_position:

    vec2 isBrick = step(norm_ppsotion, BRICK_PCT);

We can think of this as making an alpha mask, hence the name isBrick worded like a boolean. We can visualise this mask like this:

    color = vec3(isBrick.x * isBrick.y)

The reason we multiply isBrick.x by isBrick.y is to combine both into a single float value that we’ll be able to use as an alpha with the mix() function.

    color = mix(MORTAR_COLOR, BRICK_COLOR, isBrick.x * isBrick.y);

Nice.